3元神经元(SiGNN)
代办list:
- 理解RNN在GNN中的作用
- RNN的结构
SiGNN: A Spike-induced Graph Neural Network for Dynamic Graph Representation Learning
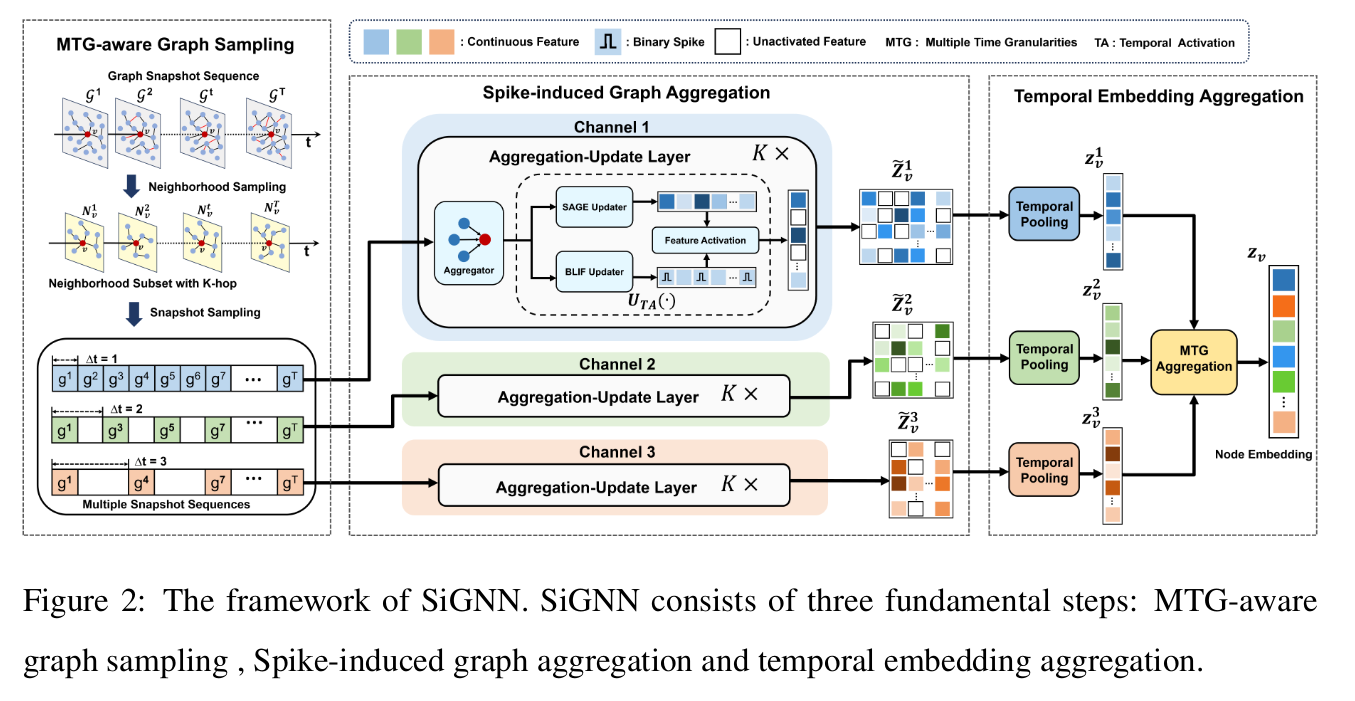
问题:上面三个步骤是所有SNNs-GNN任务都有的吗?
采用了不同粒度的感知图采样(MTG-aware Graph Sampling)
在上述的图中分别是 $\Delta t=1$,$\Delta t=2$和$\Delta t=3$,然后最后进行时间嵌入聚合。
Bidirectional LIF Neuron
Integrate: $\tilde{V}^t=V^{t-1}+\tau\left(V_{\text {reset }}-V^{t-1}+I^t\right)$
Fire : $S^t=Fb\left(\tilde{V}^t, V{t h}^{t-1}\right)$
Reset : $\quad V^t=\tilde{V}^t\left(1-S^t\right)+V_{\text {reset }} S^t$
Update: $\quad V{t h}^t=\gamma V{t h}^{t-1}+(1-\gamma) S^t$
双向监测机制:
$$
S^t=\Theta\left(\tilde{V}^t-V{t h}^{t-1}\right)+\Theta\left(-V{t h}^{t-1}-\tilde{V}^t\right)
$$
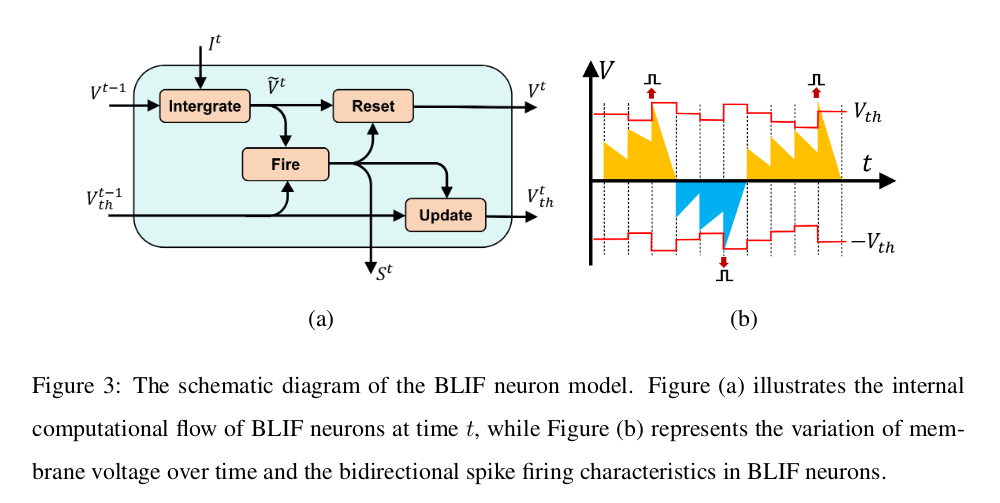
$\tilde{V}^t$可能存在负电位的情况,不止是正电位。抑制触发的阈值和正向触发阈值相同。
$$
S^t=B L I F\left(I^t ; V^{t-1}, V{t h}^t, V{\text {reset }}, \tau, \gamma\right)
$$
疑问:
$\quad V{t h}^t=\gamma V{t h}^{t-1}+(1-\gamma) S^t$是否发挥了作用,假设是抑制激活,那应该增加阈值电压,并且应该向后端发送一个-1的电位(增加阈值电压确实做到了,但是-1电位呢?)。update函数的单调性取决于$S^t$。什么情况下能触发负电位?
时态激活(我想知道不使用TA机制的是什么方法)
计算邻居隐藏层的平均
$$
\begin{aligned}
& h_{N_v}^{t,(k)}=\operatorname{Agg}\left(h_u^{t,(k)}, \forall u \in N_v^t\right) \
& hv^{t,(k+1)}=U{T A}\left(hv^{t,(k)}, h{N_v}^{t,(k)}\right)
\end{aligned}
$$
$U_{T A}(\cdot)$的采用TA机制,用下列方式更新节点表示:
$$
\begin{aligned}
\tilde{h}v^{t,(k+1)} & =\sigma\left(h{N_v}^{t,(k)} \mathbf{W}_h^{(k)}+h_v^{t,(k)} \mathbf{B}_h^{(k)}\right) \
sv^{t,(k+1)} & =B L I F\left(h{N_v}^{t,(k)} \mathbf{W}_s^{(k)}+h_v^{t,(k)} \mathbf{B}_s^{(k)}\right)
\end{aligned}
$$
在您提供的方程中:
$$
h_v^{t,(k+1)}=s_v^{t,(k+1)} \odot \tilde{h}_v^{t,(k+1)}
$$
这里的符号含义如下:
- $h_v^{t,(k+1)}$ 这是节点 v 在时间步 t 和迭代 k+1 中的状态或特征向量。它通常表示当前时间步的输出或更新后的状态。
- $s_v^{t,(k+1)}$: 如之前所述,这可能表示节点 v 在时间步 t 和迭代 k+1 中的神经元状态或特征向量,通常与神经元的激活有关。
- $\tilde{h}_v^{t,(k+1)}$: 这是节点 v 在时间步 t 和迭代 k+1 中经过某种变换(如加权和及激活函数处理)后的特征向量。
- ⊙: 这是元素级乘法(Hadamard乘积),表示两个向量相同位置元素之间的乘法。



